perkeyone
something clever
- Reaction score
- 71
im moving this to the beginning of the post said:my question to you all is...
since this method of representing multiplication can be ambiguous, what changes, if any, do you think could be made to either the syntax of multiplication or (the wording of) the order of operations to avoid said ambiguity.
i am not asking whether you think the answer is 1 or 9. i am not asking for your math professor's expert opinion. i am asking for a set of rules for which such an equation would have only one valid interpretation.
recently, as many of you may already know, several facebook polls have been created featuring ambiguously written equations, such as this one...
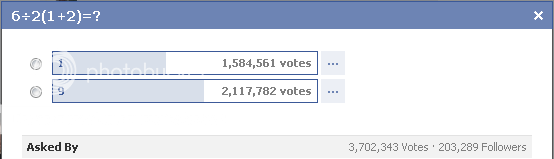
upon seeing this question, my first reaction was that there couldnt possibly be that many dumb people... i took a moment to calculate it in my head and found that i had a distinct urge to group the 2 with the parentheses (which would yield an answer of 1) but after some consideration i felt that my urge went against order of operations. i tried to verify my answer...
6÷2(1+2) - Wolfram|Alpha said:http://www.wolframalpha.com/input/?i=6÷2(1+2)

mathematica plaintext input: (6/2) (1 + 2)

mathematica plaintext output: 9
6÷2(1+2) - Google Search said:http://www.google.com/search?client...bih=685&q=6%F72%281%2B2%29&btnG=Google+Search
(6 ÷ 2) * (1 + 2) = 9
More about calculator.
Search for documents containing the terms 6÷2(1+2).

in two of these cases, the implied multiply was replaced by a multiplication symbol and in the other, a new set of parentheses was added. i was unsure whether this had any effect on the result and judging by how divided the answers on facebook were i decided to research the issue a bit. my first stop, of course was wikipedia.
wikipedia didnt seem to explicitly describe any change in operator precedence for this case, so i decided to keep looking. using the term "multiplication by juxtaposition" from the wiki article, a google search yielded several threads about this same topic. these were two of the sources they cited.Multiplication - Wikipedia said:http://en.wikipedia.org/wiki/Multiplication#Notation_and_terminology
In algebra, multiplication involving variables is often written as a juxtaposition (e.g. xy for x times y or 5x for five times x). This notation can also be used for quantities that are surrounded by parentheses (e.g. 5(2) or (5)(2) for five times two).
The Order of Operations: More Examples said:http://www.purplemath.com/modules/orderops2.htm
This next example displays an issue that almost never arises but, when it does, there seems to be no end to the arguing.
Code:* Simplify 16 ÷ 2[8 – 3(4 – 2)] + 1. 16 ÷ 2[8 – 3(4 – 2)] + 1 = 16 ÷ 2[8 – 3(2)] + 1 = 16 ÷ 2[8 – 6] + 1 = 16 ÷ 2[2] + 1 (**) = 16 ÷ 4 + 1 = 4 + 1 = 5
The confusing part in the above calculation is how "16 divided by 2[2] + 1" (in the line marked with the double-star) becomes "16 divided by 4 + 1", instead of "8 times by 2 + 1". That's because, even though multiplication and division are at the same level (so the left-to-right rule should apply), parentheses outrank division, so the first 2 goes with the [2], rather than with the "16 divided by". That is, multiplication that is indicated by placement against parentheses (or brackets, etc) is "stronger" than "regular" multiplication. Typesetting the entire problem in a graphing calculator verifies this hierarchy:

Note that different software will process this differently; even different models of Texas Instruments graphing calculators will process this differently. In cases of ambiguity, be very careful of your parentheses, and make your meaning clear. The general consensus among math people is that "multiplication by juxtaposition" (that is, multiplying by just putting things next to each other, rather than using the "×" sign) indicates that the juxtaposed values must be multiplied together before processing other operations. But not all software is programmed this way, and sometimes teachers view things differently. If in doubt, ask!
(And please do not send me an e-mail either asking for or else proffering a definitive verdict on this issue. As far as I know, there is no such final verdict. And telling me to do this your way will not solve the issue!)
so, all i really managed to find out, is that not everyone agrees on this issue.Math Forum - Ask Dr. Math said:http://mathforum.org/library/drmath/view/57021.html
...that "multiplication indicated by juxtaposition is carried out before
division." Thus, in general, for any variables a, b and c, we would
have a/bc = a/(bc) (assuming, of course, that b and c are nonzero).
Indeed, this convention is consistent with what I have seen in many
mathematical books at various levels; for example, on p. 84 of
Allendoerfer and Oakley, _Principles of Mathematics_, 1969 (my
pre-college math book), we find:
(a / b) x (c / d) = a c / b d
which is generally true only if the right side is interpreted as:
(a c) / (b d)
Notably, the above equality would *not* be generally true were we to
interpret the right side as:
[(a c) / b] d
per the first Web page above (and many others), which states that one
should "do multiplication and division as they come." However, perhaps
this page is tacitly ignoring "implicit multiplication" (by
juxtaposition) and only considering "explicit multiplication" (via
some multiplication sign) - a distinction is made at:
Order of Operations - Dr. Math Archives
http://mathforum.org/dr.math/problems/wuandheil.05.19.99.html
as a computer science major, i know that having only one valid interpretation of an expression is very important in my field, particularly when designing a compiler.
my question to you all is...
since this method of representing multiplication can be ambiguous, what changes, if any, do you think could be made to either the syntax of multiplication or (the wording of) the order of operations to avoid said ambiguity.
i am not asking whether you think the answer is 1 or 9. i am not asking for your math professor's expert opinion. i am asking for a set of rules for which such an equation would have only one valid interpretation.