Game Math; Vector Dot Product

[camelCase]

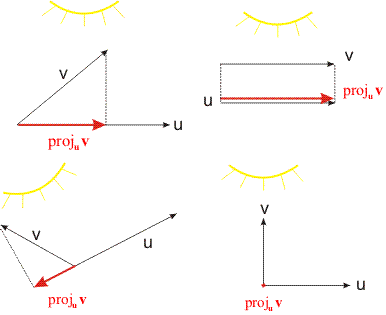
My friend recently told me about vector dot products and how you could use them to find the angle between two vectors.
Pretty useful stuff but after some thinking, I realized that I don't understand why it works at all.

So, say we've got two vectors and I do this:

Vector2D normalized_A;
Vector2D normalized_B;

//Give the two vectors some values and normalize the vectors..

float radian_between = acos(normalized_A.dotProduct(normalized_B));

radian_between now has the angle between the two vectors.

Before I knew about dot products and normalization, whenever I had to find the angle between two vectors, I would do this:

Vector2D unnormalized_A;
Vector2D unnormalized_B;

//Give the two vectors some values..
float radian_A = acos(unnormalized_A.x / unnormalized_A.length());
float radian_B = acos(unnormalized_B.x / unnormalized_B.length());

float radian_between = abs(radian_A-radian_B);

So, now that I do know about normalization and dot products..
Why does this:

Vector2D normalized_A;
Vector2D normalized_B;

//Give the two vectors some values and normalize the vectors..

float radian_between = acos(normalized_A.dotProduct(normalized_B));

Produce the same result as this:

Vector2D normalized_A;
Vector2D normalized_B;

//Give the two vectors some values and normalize the vectors..
float radian_A = acos(normalized_A.x);
float radian_B = acos(normalized_B.x);

float radian_between = abs(radian_A-radian_B);

Like, dotProduct() is really:

float Vector2D::dotProduct (Vector2D const& other) {
    return x*other.x + y*other.y;
}

I don't see why "acos(x*other.x+y*other.y)" is equal to "abs(acos(x) - acos(other.x))".
I'm not sure if I'm really asking my question correctly =/

Okay..
Given two normalized vectors..
I can understand why the dot product always gives a value between -1.0 and 1.0..
What I don't get is why the dot product of the two normalized vectors will give a scalar that just so conveniently happens to give the angle between the two vectors when fed into the arc-cosine function.

 

[Artificial]

The definition of the dot product says x·y = |x| |y| cos θ (where |a| means the length of the vector a and θ is the angle between the vectors). Because the vectors are normalized, their lengths are 1 so the equation is reduced to x·y = cos θ. Because cos(a) = b ⇔ a = arccos(b) the equation is equivalent to arccos(x·y) = θ.

The definition of the dot product also says that x·y = x[sub]i[/sub]y[sub]i[/sub] + x[sub]j[/sub]y[sub]j[/sub] (which is what you've used), so we can put that into the previous equation and get arccos(x[sub]i[/sub]y[sub]i[/sub] + x[sub]j[/sub]y[sub]j[/sub]) = θ. So no magic going on here, the result comes directly from the definitions of arccos and the dot product.

 

[camelCase]

Oh....................
So the dot product of two normalized vectors always returns -1.0 to 1.0 because cos() only returns values from -1.0 to 1.0..

Thanks for the help, Artificial!

I also did a bit more searching because I didn't know why it was defined that way..
Turns out, that definition came from the cosine rule which came from the pythagorean theorem which came from similarity O_O

Wish I had started learning math much sooner =/

 

[UnknowVector]

Looks like you've got physics code up there. That's pretty much how I learned about dot products myself.

You might know all this already, but here's some more stuff about the dot product. The internet can't possibly have too many posts about the dot product, given how important it is.

The dot product of a vector a with a unit vector b is equal to the magnitude of the projection of a in the direction of b.

http://algebra.nipissingu.ca/tutorials/vectors.html

This also just follows from the definition of the dot product:
a · b = |a| * |b| * cos(θ)
... when b is a unit vector ...
a · b = |a| * cos(θ) = magnitude of projection a onto unit vector b
see the picture below:

http://en.wikipedia.org/wiki/Fileot_Product.svg
easy trig!

So the dot product of two normalized vectors always returns -1.0 to 1.0 because cos() only returns values from -1.0 to 1.0

Yes, but there's another explanation too. If you want the longest projection of a onto unit vector b possible, then you need to point a in the same direction as b (or directly opposite b). In this situation, the projection is as long as a itself (in fact the projection is a). So the dot product, being the magnitude of the projection, can never be larger than the magnitude of a. If a is ALSO a unit vector, then the dot product can never be larger than 1, because 1 is the magnitude of a.
a · b = |a| * cos(θ)
|a| gives the maximum possible length of the projection, and cos(θ) either does nothing or makes the projection smaller because the angle between the vectors is non-zero (and it can also flip the projection around).

The magnitude of the projection of a onto any vector b, regardless of whether it's a unit vector or not, is just a dotted with the normalized form of b.
magnitude of projection a onto b = (a · normalized b) = (a · (b / |b|)).

You can also talk about the projection of a onto b, as opposed to just the magnitude of the projection. To get that, just take the magnitude and multiply it by the unit vector in the b direction

projection a onto unit vector b = (a · b) * b
projection a onto any vector b = (a · normalized b) * (normalized b) = (a · (b / |b|)) * (b / |b|)

This formula is easy to remember:
a · b = a.x*b.x + a.y*b.y
This one is hard to remember but equally important:
a · b = |a| * |b| * cos(θ)
If it helps, think of the "dot-cos bubble" . That works for me at least.

 

[camelCase]

I got lost somewhere in between..
Okay..
Say I've got two vectors..
Vector a = 2, 1
Vector b = 4, 3

magnitude of projection a onto b = (a · normalized b) = (a · (b / |b|))
= (2, 1) . ((4, 3) / 25)
= (2, 1) . (0.16, 0.12)
= 2*0.16 + 1*0.12
= 0.32 + 0.12
= 0.44

Projection "a" onto any vector "b" = (a . normalized b) * (normalized b) = (a · (b / |b|)) * (b / |b|)
= ((2, 1) . ((4, 3) / 25)) * ((4, 3) / 25)
= ((2, 1) . (0.16, 0.12)) * (0.16, 0.12)
= (2*0.16)+(1*0.12) * (0.16, 0.12)
= (0.32+0.12) * (0.16, 0.12)
= (0.44) * (0.16, 0.12)
= (0.0704, 0.0528)

Length of (0.0704, 0.0528) = sqrt((0.0704*0.0704) + (0.0528*0.0528))
= 0.088

I don't get the "Projection a onto any vector b" bit.

 

[phyrex1an]

You're using the wrong definition of |b| in both calculations.

b = 4,3
|b| = sqrt(4*4+3*3) = sqrt(25) = 5

 

[camelCase]

Gah!
Got it =x